Our topic this week is the properties of diagnostic tests, and their implications for interpreting test results.

Suppose that we want to know if a person has a urinary tract infection. Their white blood cell count seems higher than that of the average patient, but there's natural variation in this number, and it's not impossible that a healthy patient could have a WBC that high. We might describe the situation graphically like this:

As the WBC gets higher, the person is more likely to be sick, and as its lower, they're more likely to be healthy. Whatever criterion we set for calling someone sick or healthy based on this test, there will be some people rightly classified as sick or healthy, and some people wrongly classified as sick or healthy. The higher the WBC we require in order to call someone sick, the more we'll wrongly classify sick people as healthy, but the lower the WBC we require, the more we'll wrongly classify healthy people as sick. The decision about where to set our criterion for calling someone healthy or sick based on their WBC is an interesting one that we'll come back to in a later session. For now, though, let's assume that we've chosen a criterion (or one has been chosen for us), and that we simply judge people to be "high WBC" or "low WBC".

We run our test on a big group of people with and without urinary tract infections, and put the results into 2x2 tables like this:

This is a chart that you might make as part of the computer exercise for this week. Try that now, and let's take a look at the two-by-two table. What can you read off the table?

• Number of TP, FP, FN, TN: These entries are in the cells of the table
• Prevalence of disease: The total number with UTI, divided by the total number of patients gives you the prevalence of the disease
• Sensitivity and specificity (rate of TP and TN): The sensitivity is the true positive rate: the number of TPs divided by the number of people with the disease (how many sick people did the test pick up?) The specificity is the TN rate: the number of TNs divided by the number of people w/o the disease (how many health people did the test call healthy?)
• Predictive value of positive and negative test: The predictive value of a positive test (PVP) is the number of TPs divided by the overall number of positive tests (if you get a positive test, how likely is it to be a true positive?). Similarly, the PVN is the number of TNs divided by the overall number of negative tests (if you get a negative test, how likely is it to be a true negative?). Note that these numbers are different from sensitivity and specificity - many people confuse them. PVP and PVN depend on sensitivity and specificity, but also on how prevalence or rare the disease is.
• Percent correct (accuracy): Overall, how often does the test classify people correctly? This is the number of TPs plus TNs, divided by the total number of people tested. This tells you how likely you are to make some mistake with the test, but doesn't distinguish between false positives and false negatives, which often have very different implications.

Ideally, tests would be both sensitive and specific; in practice, there is often a choice between a more sensitive test and a more specific test. A useful mnemonic for determining when you'd like a sensitive test vs. a specific test is "SPIN and SNOUT." SPIN stands for "SPecific tests rule IN the condition when they're positive." SNOUT stands for "SeNsitive tests rule OUT the condition when they're negative." A specific test is rarely results in false alarms, so a positive result on a specific test is good evidence for a condition. A sensitive test rarely misses a condition, so a negative result on a sensitive test is good evidence against the condition.

Even before a test is ordered, we have some idea of how likely it is that the patient has the disease. For example, we may know that the prevalence of carpal tunnel syndrome among inpatients is 1%. This represents our best guess about whether a patient has carpal tunnel before we've seen the patient. It's called a "prior probability" -- prior to testing.

Now we learn that the patient has hand pain at night. This is a symptom of carpal tunnel syndrome, but also a symptom of other conditions. Moreover, a few people with CT don't have night pain. So, it's an uncertain indicator. The sensitivity of night pain as a test for CT is 0.71; the specificity is 0.995. With this additional information, how likely is it that our patient has CT? That is, what is the "posterior probability" -- after testing?

The way to calculate the posterior is with Bayes' theorem, a formula that comes directly from the rules of probability theory. It says:

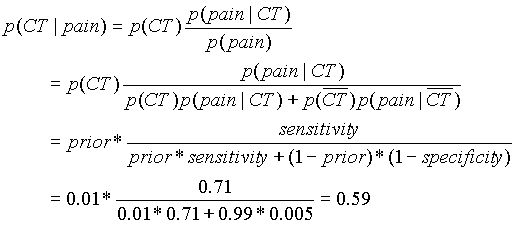
Before the test, our best guess was a 0.01 probability. Now that we know that the patient has hand pain, we can revise or update this probability to 0.59. Notice that the probably is not 0.71 after a positive test -- we can't ignore the fact that the prior probability is low and makes the condition less likely. To convince yourself of that, consider a test for smallpox. Smallpox is an effectively extinct disease in the U.S. -- the prevalence is 0%. Moreover, suppose we have a very good diagnostic test with sensitivity and specificity of 99%, and we run it on 100,000 people. We expect to find 1,000 (false) positive test results. How likely is it that these people have smallpox? Clearly not 0.99 -- in fact, we know that the answer is 0, and Bayes' theorem will correctly give 0 as the answer.